【Unity】HLSLに入門（おもちゃラボさんの記事を読んで。）

はじめに

読んでね。 nn-hokuson.hatenablog.com

できたやつ

学んだことメモ

上のナンバリングに沿ってシェーダを記載。

①

         fixed4 frag(v2f i) : SV_Target
            {
                fixed4 black = fixed4(.1, .1, .1, 1.);
                fixed4 red  = fixed4(.9, .2, .1, 1.);
                float x = step(.2, i.uv.x) * step(.2, 1. - i.uv.x);
                float y = step(.2, i.uv.y) * step(.3, 1. - i.uv.y);
                return lerp(black, red, x * y);
            }

ボックス。
よく使うstep関数。i = step(a, x) で i = (x > a) ? 1.0 : 0.0 になる。
lerp関数はglslでいうmix関数。つまり、 i = lerp(a, b, x) => i = mix(a, b, x) => x(0.0 ~ 1.0)を(a,b)間で線形補間 => i = a + x * (b - a) となる。

②

            fixed4 frag (v2f i) : SV_Target
            {
                fixed r1 = .11;
                fixed r2 = .13;
                fixed r3 = .08;
                fixed2 c1 = fixed2(.5, lerp(.5, .1, _SinTime.x ));
                fixed2 c2 = fixed2(.2, lerp(.7, .2, _SinTime.y ));
                fixed2 c3 = fixed2(.7, lerp(.4, .2, _SinTime.z ));
                fixed d1 = distance(i.uv, c1);
                fixed d2 = distance(i.uv, c2);
                fixed d3 = distance(i.uv, c3);

                return smoothstep(r1, r1 * 1.1, d1) 
                     * smoothstep(r2, r2 * 1.1, d2) 
                     * smoothstep(r3, r3 * 1.1, d3);
            }

長々しく書いていますが、やっていることは動く円３つを書いているだけです。ポイント、というか「へぇ～」となったのは_SinTime というか _Time 含めた時間に関するHLSLのビルドイン変数についてです。これらは float4 の型を持っています。最初これがわからずエラーを出していました。以下の表は公式のマニュアルによるもの。

名前	タイプ	値
_Time	float4	ステージのロードからの時間 (t/20, t, t2, t3)。
_SinTime	float4	時間の正弦: (t/8, t/4, t/2, t)
_CosTime	float4	時間の余弦: (t/8, t/4, t/2, t)
unity _DeltaTime	float4	デルタ時間: (dt, 1/dt, smoothDt, 1/smoothDt)

_Time.x や _CosTime.y みたいな形で使う模様。ほへ～。覚えておく。

③

            fixed4 frag (v2f i) : SV_Target
            {
                fixed len = distance(i.uv, fixed2(.5, .5)) + _Time;
                fixed4 red = fixed4(.9, .2, .1, 1.);
                return red * (1.0 - smoothstep(.5, .9, sin(len *40)));
            }

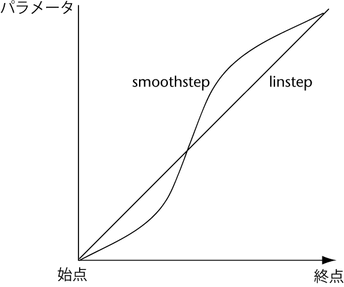
②にも出てきたdistance関数とsmoothstep関数。distanceは名前そのまま。２点の距離を返す。distance(P.xy, Q.xy)。smoothstepもGLSLで頻繁に使う。smoothstep(min, max, a) min ~ max間でaの値をエルミート補間する。エルミート補間？ という人は下の図で理解できるかと。

④

            fixed4 frag (v2f i) : SV_Target
            {
                return step(abs(.4 * cos(_Time.y)), sin(50*i.uv.x));
            }

特にコメントなし。

⑤

            fixed4 frag (v2f i) : SV_Target
            {
                fixed2 st = i.uv * 4;
                st = frac(st);
                fixed d = distance(st, fixed2(.5,.5));
                return smoothstep(.4, .42, d);
            }

最初の２行が肝だと思う。1:1スケールをN倍してfrac（小数だけ見る）させることで0.0 ~ 1.0をN回繰り返すスケールを得る。こうすることでN*Nマスで表現の繰り返しを描ける。便利。

⑥

            fixed4 frag (v2f i) : SV_Target
            {
                fixed2 v = step(0, sin(25 * i.uv)) / 2;
                fixed4 f = frac(v.x + v.y) * 2;
                fixed r = lerp(.1, .2, _SinTime.z);

                fixed4 black = fixed4(.9, .9, .9, 1.);
                fixed4 red  = fixed4(.9, .2, .1, 1.);
                fixed4 c1 = smoothstep(r,r * 1.05, distance(i.uv, fixed2(.315,.31)));
                fixed4 c2 = smoothstep(r,r * 1.05, distance(i.uv, fixed2(.695,.69)));
                return f * lerp(black, red, (c1 * c2));
            } 

これはおもちゃラボさんの解説がわかりやすかった。縦横のストライプを 0.0 or 0.5 で表現してそれぞれ加算してfracさせれば市松模様になるというもの。

⑦

            fixed4 frag (v2f i) : SV_Target
            {
                return smoothstep(.1,.4, 1. - i.uv.y) * smoothstep(.1,.4, 1. - i.uv.x);
            }

これも説明不要かと。smoothstepのsmoothさがよくわかりますね。

⑧

                fixed2 st = i.uv * 3;
                st = frac(st);
                fixed4 black = fixed4(.1, .1, .1, 1.);
                fixed4 red  = fixed4(.9, .2, .1, 1.);
                fixed side = lerp(.3, .6, _SinTime.w);
                float x = step(side, st.x) * step(.3, 1. - st.x);
                float y = step(side, st.y) * step(.4, 1. - st.y);
                return lerp(red, black, x * y);

そうです、①×⑤の作品です。

---

ということであらためておもちゃラボさんの入門記事がよかったです。皆さんも是非。

参考

knowledge.autodesk.com