あけましておめでとうございます。
■ 今回のきっかけ
新年を迎えても相変わらずだらだらとp5.jsをいじっていてふと気になったことがありました。
それは「curve()関数とbezier()関数の引数の順番がややこしい」ということです。
P1(x1, y1) ... 開始点
P2(x2, y2) ... 終点
C1(cx1, cy1) ... 開始点側の制御点
C2(cx2, cy2) ... 終点側の制御点
としたとき(それぞれがどういう意味を持つかは後ほど)に、
curve(cx1, cy1, x1, y1, x2, y2, cx2, cy2)
curve() - Reference p5.js
というような順番であるのに対して、
bezier(x1, y1, cx1, cy1, cx2, cy2, x2, y2)
bezier() - Reference p5.js
みたいな感じなんですよね。
これのせいで気軽にcurve()関数をbezier()関数に置換させることができません。
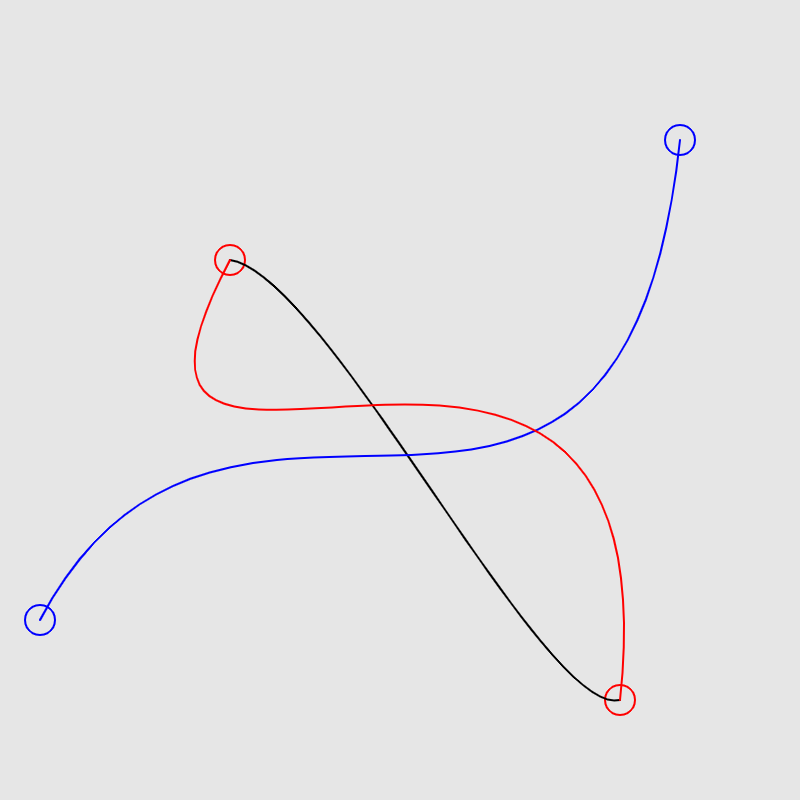
function setup() {
createCanvas(400, 400);
background(230);
}
function draw() {
noLoop();
noFill();
var r = 15;
stroke("red");
circle(115, 130, r);
circle(310, 350, r);
stroke("blue");
circle(20, 310, r);
circle(340, 70, r);
stroke("black");
curve(20, 310, 115, 130, 310, 350, 340, 70);
stroke("blue");
bezier(20, 310, 115, 130, 310, 350, 340, 70);
stroke("red");
bezier(115, 130, 20, 310, 340, 70, 310, 350);
}
本当は関数を置換するだけで黒線(curve()関数)を赤線(bezier()関数)のようにしたい(のに、青線になってしまう…)。
という、どうでもいい細かいところに引っかかったところから
「そもそもベジェ曲線ってどうなってるの?」
「p5.jsだけでなくIllustratorやPhotoshopなんかのAdobe製品でも出てくるし?」
「CADとかも使わないけど、たしか関係あるよね?」
など疑問が湧いてきたのでベジェ曲線について調べてみました。
■ そもそも線分とは?
ベジェ曲線のアルゴリズムについて調べたとき、おそらく検索結果のトップ3のうち1つはこちらの記事「一から学ぶベジェ曲線」(日本語)かと思います。(この記事を読む前に一読することを勧めます。)
もともとサンフランシスコに住んでいるエンジニアの方が書かれたこちらの記事Bezier Curves from the Ground Up - Zero Wind(英語)があるので、英語が得意な方はそちらを読まれるのが良いかと思います。
まずは、記事にもあるように2点を指す位置ベクトルに対して、それを t : (1-t) (0≦t≦1) で内分する点の集合という観点で「線分」を定義します。

 GIF1
GIF1
var time = 0;
var t = 0;
function setup() {
createCanvas(400, 400);
}
function draw() {
clear();
background(230);
noFill();
var P0 = createVector(70, 110);
var P1 = createVector(300, 310);
Setting(2, "black");
line(P0.x, P0.y, P1.x, P1.y);
text("P0", P0.x - 10,P0.y - 10);
text("P1", P1.x + 10,P1.y + 10);
time += 0.02;
t = (1 - cos(time)) / 2;
var P2 = p5.Vector.mult(P0,1-t);
var P3 = p5.Vector.mult(P1,t);
var P = P2.add(P3);
Setting(4, "red");
line(P0.x, P0.y, P.x, P.y);
Setting(1, "black");
circle(P0.x, P0.y, 5);
circle(P1.x, P1.y, 5);
Setting(1, "blue");
circle(P.x, P.y, 8);
Setting(0, "black");
var s = "t = " + t.toFixed(2);
textSize(25);
text(s, 20,30);
}
function Setting(w, color) {
strokeWeight(w);
fill(color);
stroke(color);
}
そして、今度は点を1つ増やして2つの線分それぞれに対して同じように任意の比率の内分点の集合として線分を引いてみます。

 GIF2
GIF2
var time = 0;
var t = 0;
function setup() {
createCanvas(400, 400);
}
function draw() {
clear();
background(230);
var P0 = createVector(70, 110);
var P1 = createVector(300, 310);
var P2 = createVector(350, 120);
time += 0.02;
t = (1 - cos(time)) / 2;
var Q0 = p5.Vector.mult(P0,1-t);
var Q1 = p5.Vector.mult(P1,t);
var Q = Q0.add(Q1);
var R0 = p5.Vector.mult(P1,1-t);
var R1 = p5.Vector.mult(P2,t);
var R = R0.add(R1);
Setting(2, "black");
line(P0.x, P0.y, P1.x, P1.y);
line(P1.x, P1.y, P2.x, P2.y);
Setting(4, "red");
line(P0.x, P0.y, Q.x, Q.y);
line(P1.x, P1.y, R.x, R.y);
Setting(1, "black");
circle(P0.x, P0.y, 8);
circle(P1.x, P1.y, 8);
circle(P2.x, P2.y, 8);
text("P0", P0.x - 10, P0.y - 10);
text("P1", P1.x + 10, P1.y + 10);
text("P2", P2.x - 10, P2.y - 10);
Setting(1, "blue");
circle(Q.x, Q.y, 8);
circle(R.x, R.y, 8);
text("Q", Q.x - 10, Q.y - 10);
text("R", R.x + 10, R.y + 10);
Setting(0, "black");
var s = "t = " + t.toFixed(2);
textSize(25);
text(s, 20,30);
}
function Setting(w, color) {
strokeWeight(w);
fill(color);
stroke(color);
}
さらに先程の求めたQ点,R点に対して同じように t : (1-t) (0≦t≦1) で内分させた点Sをプロットすると、なんと曲線が描けます。

これが2次のベジエ曲線と呼ばれるものです。
(つまり、1次のベジエ曲線とは定義上では直線を描くものとなります。)
 GIF3
GIF3
var time = 0;
var t = 0;
var sArray = [];
function setup() {
createCanvas(400, 400);
}
function draw() {
clear();
background(230);
var P1 = createVector(70, 110);
var P2 = createVector(300, 310);
var P3 = createVector(350, 120);
text("P0", P1.x - 10, P1.y - 10);
text("P1", P2.x - 10, P2.y - 10);
text("P2", P3.x - 10, P3.y - 10);
time += 0.02;
var t_prev = t;
t = (1 - cos(time)) / 2;
var Q = calc(P1, P2, t);
var R = calc(P2, P3, t);
var S = calc(Q, R, t);
if(t_prev < t) {
sArray.push(S);
} else {
sArray.pop(S);
}
Setting(2, "black");
line(P1.x, P1.y, P2.x, P2.y);
line(P2.x, P2.y, P3.x, P3.y);
line(Q.x, Q.y, R.x, R.y);
Setting(4, "red");
line(P1.x, P1.y, Q.x, Q.y);
line(P2.x, P2.y, R.x, R.y);
line(Q.x, Q.y, S.x, S.y);
for(let i = 0; i < sArray.length; i++) {
Setting(1, "yellow");
var dS = sArray[i];
circle(dS.x, dS.y, 3);
}
Setting(1, "black");
circle(P1.x, P1.y, 5);
circle(P2.x, P2.y, 5);
circle(P3.x, P3.y, 5);
Setting(1, "blue");
circle(Q.x, Q.y, 8);
circle(R.x, R.y, 8);
circle(S.x, S.y, 8);
text("Q", Q.x - 10, Q.y - 10);
text("R", R.x - 10, R.y - 10);
text("S", S.x + 5, S.y + 30);
Setting(0, "black");
UpdateText(t);
}
function UpdateText(t) {
var s = "t = " + t.toFixed(2);
textSize(25);
text(s, 20,30);
}
function Setting(w, color) {
strokeWeight(w);
fill(color);
stroke(color);
}
function calc(leftP, rightP, t) {
var n = p5.Vector.mult(leftP,1-t);
var m = p5.Vector.mult(rightP,t);
return n.add(m);
}
点を1つ増やす(次数を上げる)ことで3次のベジェ曲線も簡単に描けます。
ここまでの数式から3次のベジェ曲線のベクトル方程式は以下のように導けます。

GIF4の細いピンクの線はp5.jsのbezier()関数の結果です。
 GIF4
GIF4
var time = 0;
var t = 0;
var sArray = [];
function setup() {
createCanvas(400, 400);
}
function draw() {
clear();
background(230);
var P1 = createVector(40, 70);
var P2 = createVector(90, 280);
var P3 = createVector(290, 320);
var P4 = createVector(350, 110);
textSize(24);
text("P0", P1.x - 10, P1.y - 10);
text("P1", P2.x + 5, P2.y + 30);
text("P2", P3.x + 5, P3.y + 30);
text("P3", P4.x - 10, P4.y - 10);
textSize(12);
strokeWeight(2);
noFill();
stroke("pink");
bezier(40, 70, 90, 280, 290, 320, 350, 110);
time += 0.02;
var t_prev = t;
t = (1 - cos(time)) / 2;
var Q1 = calc(P1, P2, t);
var Q2 = calc(P2, P3, t);
var Q3 = calc(P3, P4, t);
var R1 = calc(Q1, Q2, t);
var R2 = calc(Q2, Q3, t);
var S1 = calc(R1, R2, t);
if(t_prev < t) {
sArray.push(S1);
} else {
sArray.pop(S1);
}
for(let i = 0; i < sArray.length; i++) {
var dS = sArray[i];
Setting(3, "yellow");
circle(dS.x, dS.y, 3);
}
Setting(2, "black");
circle(P1.x, P1.y, 8);
circle(P2.x, P2.y, 8);
circle(P3.x, P3.y, 8);
circle(P4.x, P4.y, 8);
line(P1.x, P1.y, P2.x, P2.y);
line(P2.x, P2.y, P3.x, P3.y);
line(P3.x, P3.y, P4.x, P4.y);
Setting(3, "red");
line(P1.x, P1.y, Q1.x, Q1.y);
line(P2.x, P2.y, Q2.x, Q2.y);
line(P3.x, P3.y, Q3.x, Q3.y);
Setting(4, "blue");
circle(Q1.x, Q1.y, 8);
circle(Q2.x, Q2.y, 8);
circle(Q3.x, Q3.y, 8);
Setting(1, "blue");
text("Q0", Q1.x - 20, Q1.y - 20);
text("Q1", Q2.x - 20, Q2.y - 20);
text("Q2", Q3.x - 20, Q3.y - 20);
Setting(2, "black");
line(Q1.x, Q1.y, Q2.x, Q2.y);
line(Q2.x, Q2.y, Q3.x, Q3.y);
Setting(3, "red");
line(Q1.x, Q1.y, R1.x, R1.y);
line(Q2.x, Q2.y, R2.x, R2.y);
Setting(4, "blue");
circle(R1.x, R1.y, 8);
circle(R2.x, R2.y, 8);
Setting(1, "blue");
text("R0", R1.x + 10, R1.y + 30);
text("R1", R2.x + 10, R2.y + 30);
Setting(2, "black");
line(R1.x, R1.y, R2.x, R2.y);
Setting(3, "red");
line(R1.x, R1.y, S1.x, S1.y);
Setting(4, "white");
circle(S1.x, S1.y, 8);
Setting(1, "white");
textSize(24);
text("S", S1.x, S1.y - 15);
Setting(0, "black");
UpdateText(t);
}
function UpdateText(t) {
var s = "t = " + t.toFixed(2);
textSize(25);
text(s, 20,30);
}
function Setting(w, color) {
strokeWeight(w);
fill(color);
stroke(color);
}
function calc(leftP, rightP, t) {
var n = p5.Vector.mult(leftP,1-t);
var m = p5.Vector.mult(rightP,t);
return n.add(m);
}
1,2,3次のベジェ曲線の方程式から一般化させたn次のベジェ曲線の定義式が以下です。

この場合、制御点の数は(n+1)個であることに注意してください。(1次のベジェ曲線が2点を結ぶ線分だったことを思い出しましょう。)
n_C_iはいわゆる二項係数と呼ばれるもので、それを使ったB(t) のような関数をバーンスタイン基底関数と呼ぶそうです。
ここでは背景にある数学的面白さはひとまず横においておくとして、定義がわかったのでアルゴリズム(ベジエ氏より以前にこのアルゴリズムを発見した人にあやかって「ド・カステリョのアルゴリズム」と呼ばれている)をプログラムに落とし込んでいきたいと思います。
※ちなみに「ド・カステリョのアルゴリズム」含めより詳細なベジェ曲線についての説明を読みたい方はこちらの「A Primer on Bézier Curves(ベジェ曲線入門)」という無料の電子書籍サイトが参考になるかと思います。(僕は途中で読むのを断念しました。)
くどくど書いてきましたが実装は非常にシンプルになります。
(折りたたんでいたソースコードを読んでくださった人はわかると思いますが、ここまでの実装はすべて1つずつ計算する力技でした。)
 GIF5
GIF5
var time = 0;
var t = 0;
function setup() {
createCanvas(400, 400);
}
function draw() {
clear();
background(230);
var P1 = createVector(40, 70);
var P2 = createVector(90, 280);
var P3 = createVector(290, 320);
var P4 = createVector(350, 110);
Setting(1, "blue");
circle(P1.x, P1.y, 8);
circle(P2.x, P2.y, 8);
circle(P3.x, P3.y, 8);
circle(P4.x, P4.y, 8);
Setting(1, "black");
text("P0", P1.x - 10, P1.y - 10);
text("P1", P2.x - 10, P2.y - 10);
text("P2", P3.x - 10, P3.y - 10);
text("P3", P4.x - 10, P4.y - 10);
strokeWeight(2);
noFill();
stroke("black");
bezier(40, 70, 90, 280, 290, 320, 350, 110);
time += 0.02;
var t_prev = t;
t = (1 - cos(time)) / 2;
var points = [P1, P2, P3, P4];
var P = Calc(points, t);
strokeWeight(1);
noFill();
stroke("red");
circle(P.x, P.y, 16);
Setting(0, "black");
UpdateText(t);
}
function UpdateText(t) {
var s = "t = " + t.toFixed(2);
textSize(25);
text(s, 20,30);
}
function Setting(w, color) {
strokeWeight(w);
fill(color);
stroke(color);
}
function Calc(points, t) {
var cx = 0, cy = 0;
var n = points.length;
for (let i = 0; i < n; i++) {
cx += points[i].x * Bernstein(n - 1, i, t);
cy += points[i].y * Bernstein(n - 1, i, t);
}
var res = createVector(cx, cy);
return res;
}
function Bernstein(n, i, t) {
return Biominal(n, i) * pow(t, i) * pow(1-t, n-i);
}
function Biominal(n ,k) {
return Factorial(n) / (Factorial(k) * Factorial(n-k));
}
function Factorial(n) {
var res = 1;
for(let i = 2; i <= n; i++) {
res *= i;
}
return res;
}
いかがでしょうか。黒線がp5.jsで書いたベジェ曲線。赤丸が移動している軌跡が今回実装したベジェ曲線になります。
念の為、一応細かいところを解説しておくと、二項係数は以下の公式を使っています。

(高校数学を思い出しますね。)
■ ところでベジェ氏って何者?
ピエール・ベジェ氏は、フランスの自動車会社「ルノー」に所属していたエンジニアで1972年に車体の形状の設計をするにあたり、このベジェ曲線を提案・発表したようです。
ちなみに先ほど登場したド・カステリョ氏は当時同じフランスの自動車メーカーのシトロエンに在籍しており、ベジェ曲線の発表より先に研究を進めていたものの外に公表されませんでした。
そのため、現在では一般的にはベジェさんの名前が使われているという経緯があります。
■ 最初の目的見失ってない?
そうでした。そもそも今回のきっかけはp5.jsのbezier()関数の引数の順番に引っかかったところから出発しました。しかしそれもGIF4とかを見ているとすでにこの順番であることは不思議ではありません。が、一応せっかくなのでp5.jsのbezier()関数の実装を見にいきます。
p5.Renderer2D.prototype.bezier = function(x1, y1, x2, y2, x3, y3, x4, y4) {
this._pInst.beginShape();
this._pInst.vertex(x1, y1);
this._pInst.bezierVertex(x2, y2, x3, y3, x4, y4);
this._pInst.endShape();
return this;
};
p5.Renderer2D.prototype.curve = function(x1, y1, x2, y2, x3, y3, x4, y4) {
this._pInst.beginShape();
this._pInst.curveVertex(x1, y1);
this._pInst.curveVertex(x2, y2);
this._pInst.curveVertex(x3, y3);
this._pInst.curveVertex(x4, y4);
this._pInst.endShape();
return this;
};
github.com
bezierVertex()、curveVertex()がそれぞれどう定義されているかまで追いかけてもよいのですが、これだけでcurve()関数とbezier()関数の違いを理解するのには十分です。
そろそろ書くのに疲れたので主題ではないのでここでは深く追求しませんが、curve()関数の中身は「Catmull-Rom スプライン」と呼ばれる曲線です。そして、これのベースには「エルミート曲線」と呼ばれる曲線アルゴリズムを使用されています。
この「エルミート曲線」は入力に①開始点と②終点と③開始点ベクトルと④終点ベクトルの4つが必要なのですが「Catmull-Rom スプライン」は③④のベクトルの代わりに長い曲線の中の「開始点の前の点(制御点1)から開始点の次の点(=終点)への傾き」と「終点の前の点(=開始点)から終点の後の点(制御点2)への傾き」を入力に入れて中でゴニョゴニョします。(参考1 、参考2)
それがp5.js(およびProcessing)の実装における(x1, y1) と (x4,y4) の座標というわけです。「長い曲線の中の4つの点に注目している」というのがポイントです。そうなると P1(制御点)->P2(開始点)->P3(終点)->P4(制御点)のように引数の順番は(cx1, cy1, x1, y1, x2, y2, cx2, cy2)であるわけです。
一方のbezier()関数はここまでくどくど説明してきたとおり、P1(開始点)->P2(制御点)で線形補間してP3(制御点)->P4(終点)で線形補間して…とやっていくので引数の順番は(x1, y1, cx1, cy1, cx2, cy2, x2, y2)となります。
お~、読んでくださっている人に伝わっているかどうかは怪しいですが僕は非常に納得できました。
申し訳ないので上の説明のイメージ図だけ置いておきます。右がcurve()関数、左がbezier()関数です。
まとめ
すごく些細な疑問点からその背景にある興味深い数学の知識を身につけることが少しできました。
それと余談ですが、はてなブログで数式(TeX)を書く方法も今回学べました。(参考)
参考文献

 GIF1
GIF1
 GIF2
GIF2
 GIF3
GIF3
 GIF4
GIF4
 GIF5
GIF5


